Pour trouver une fonction, il est essentiel de comprendre certains termes et concepts clés. Il est important de maîtriser le vocabulaire lié aux fonctions pour faciliter leur identification et leur représentation. Une fonction est une relation entre deux ensembles de données, appelés les ensembles de départ et d’arrivée. Chaque élément de l’ensemble de départ est associé à exactement un élément de l’ensemble d’arrivée. Une fonction peut être représentée par un graphe, un tableau de valeurs ou une formule mathématique. L’expression générale d’une fonction est notée f(x) = y, où f est le nom de la fonction, x est la variable indépendante et y est la variable dépendante.
Pour commencer : un peu de vocabulaire
Une fonction affine est une fonction particulière de la forme f(x) = ax + b, où a et b sont des constantes réelles et a n’est pas égal à 0. La représentation graphique d’une fonction affine est une droite. Le coefficient a est appelé le coefficient directeur de la droite, il mesure son inclinaison par rapport à l’axe des abscisses. Quant à la constante b, elle est l’ordonnée à l’origine de la droite, c’est-à-dire l’intersection de la droite avec l’axe des ordonnées.
Définition de la fonction affine
Pour représenter une fonction affine, il existe plusieurs méthodes. La première consiste à utiliser deux points distincts de la droite représentative de la fonction. Il suffit de choisir deux points (x1, y1) et (x2, y2) appartenant à la droite, puis de tracer la droite passant par ces deux points. Une deuxième méthode consiste à utiliser le coefficient directeur a et l’ordonnée à l’origine b pour tracer la droite. Le coefficient a donne l’inclinaison de la droite, tandis que l’ordonnée à l’origine b donne le point où la droite intersecte l’axe des ordonnées.
Comment représenter une fonction affine ?
À l’aide de deux points
Pour représenter une fonction affine à l’aide de deux points, on peut suivre les étapes suivantes :
- Choisir deux points distincts (x1, y1) et (x2, y2) appartenant à la droite de la fonction affine.
- Tracer la droite passant par ces deux points.
Avec le coefficient directeur et de l’ordonnée à l’origine
Pour représenter une fonction affine à l’aide du coefficient directeur a et de l’ordonnée à l’origine b, on peut procéder comme suit :
- Utiliser le coefficient a pour déterminer l’inclinaison de la droite.
- Utiliser l’ordonnée à l’origine b pour déterminer le point d’intersection avec l’axe des ordonnées.
La détermination d’une fonction affine peut se faire de deux manières. La première méthode consiste à utiliser deux points distincts sur le graphique représentatif de la fonction. Une fois les coordonnées de ces deux points connues, le coefficient directeur et l’ordonnée à l’origine peuvent être trouvés. La deuxième méthode consiste à déterminer l’expression d’une fonction affine à partir d’un calcul, sans avoir recours à un graphique.
Comment déterminer une fonction affine ?
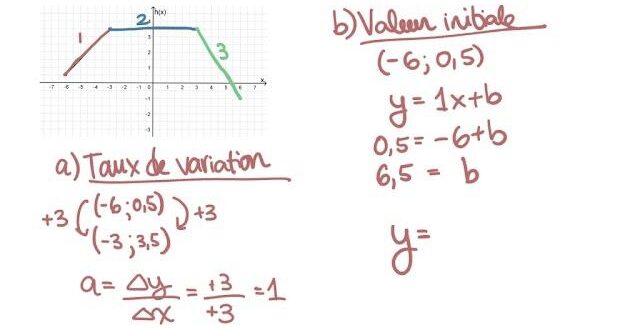
À partir de deux points sur un graphique
Pour déterminer une fonction affine à partir de deux points sur un graphique, il faut suivre les étapes suivantes :
- Calculer le coefficient directeur a à partir des coordonnées des deux points.
- Calculer l’ordonnée à l’origine b en utilisant l’une des paires de coordonnées connue.
Déterminer l’expression d’une fonction affine à partir d’un calcul
Pour déterminer l’expression d’une fonction affine à partir d’un calcul, on peut suivre les étapes suivantes :
- Utiliser les coordonnées d’un point de la droite et le coefficient directeur pour écrire l’équation de la droite.
- Résoudre l’équation pour trouver l’ordonnée à l’origine.
La fonction linéaire est un cas particulier de la fonction affine, caractérisée par un coefficient a égal à 0. Ainsi, l’expression générale d’une fonction linéaire est f(x) = b. Dans ce cas, la représentation graphique est une droite parallèle à l’axe des abscisses, c’est-à-dire une droite horizontale. Le coefficient b est l’ordonnée à l’origine de la droite.
Cas particulier de la fonction affine : la fonction linéaire
Définition de la fonction linéaire
Une fonction linéaire est une fonction affine particulière définie par f(x) = b, où b est un nombre réel. La représentation graphique d’une fonction linéaire est une droite horizontale passant par le point (0, b).
Déterminer le coefficient d’une fonction linéaire
Le coefficient d’une fonction linéaire est égal à 0, car la fonction linéaire est caractérisée par un coefficient a nul dans la forme générale f(x) = ax + b.
Représenter une fonction linéaire
La représentation graphique d’une fonction linéaire consiste en une droite horizontale passant par l’ordonnée à l’origine b.
Synthèse sur les fonctions affines 
| Titre | Contenu |
|---|---|
| Définition de la fonction affine | Forme générale f(x) = ax + b, a ≠ 0. Représentation graphique : droite. |
| Comment représenter une fonction affine ? | À l’aide de deux points ou avec le coefficient directeur et l’ordonnée à l’origine. |
| Comment déterminer une fonction affine ? | À partir de deux points sur un graphique ou à partir d’un calcul. |
| Cas particulier de la fonction affine : la fonction linéaire | Caractérisée par f(x) = b, représentation graphique : droite horizontale. |
Leçons apprises: La fonction affine est l’une des fonctions mathématiques les plus couramment rencontrées. Comprendre sa définition, sa représentation graphique et les méthodes de détermination est essentiel pour résoudre des problèmes mathématiques variés. La fonction linéaire, en tant que cas particulier de la fonction affine, présente des propriétés spécifiques qui la rendent facilement identifiable. En maîtrisant ces concepts, on peut aborder des problèmes de mathématiques et de sciences avec plus de confiance.
FAQ
Comment déterminer fonction ?
Une fonction est déterminée par une règle qui associe à chaque élément d’un ensemble donné (l’ensemble de départ ou domaine) exactement un élément d’un autre ensemble (l’ensemble d’arrivée ou codomaine). Cette règle peut être définie par une formule mathématique, une représentation graphique, un tableau de valeurs, etc.
Comment trouver une fonction à partir de 2 points ?
Pour trouver une fonction à partir de deux points, il faut d’abord calculer la pente (ou coefficient directeur) de la fonction qui est égale à (y2 – y1) / (x2 – x1). Ensuite, on utilise la formule de la fonction affine y = mx + p pour déterminer l’ordonnée à l’origine p en remplacant dans cette formule x et y par les coordonnées d’un des deux points et m par la pente trouvée précédemment.