# Comment trouver une fonction : les bases à connaître Pour comprendre comment trouver une fonction, il est essentiel de maîtriser quelques termes de base. Une fonction est une correspondance mathématique qui associe à chaque élément d’un ensemble de départ un seul élément dans un ensemble d’arrivée. Elle se symbolise généralement par f(x) = y, où x est l’entrée et y la sortie. Une fonction affine est un type particulier de fonction pour laquelle le taux de variation est constant. Enfin, une fonction linéaire est une sous-catégorie de la fonction affine, caractérisée par l’absence d’ordonnée à l’origine. #
Définition de la fonction affine
La fonction affine se caractérise par une écriture sous forme ax + b, où a et b sont des constantes réelles, avec a différent de zéro. Cette fonction est donc linéaire, mais avec une translation. Autrement dit, une fonction affine peut se représenter graphiquement avec une droite qui n’est pas nécessairement passant par l’origine du repère. Par exemple, la fonction f(x) = 2x + 3 est une fonction affine avec un coefficient directeur de 2 et une ordonnée à l’origine de 3. #
Comment représenter une fonction affine ?
Pour représenter une fonction affine, on peut utiliser différentes méthodes. ## À l’aide de deux points La première méthode consiste à choisir deux points distincts du plan et de tracer la droite passant par ces deux points. Par la suite, on obtient une droite représentative de la fonction affine. Cette méthode est la plus couramment utilisée pour représenter visuellement une fonction affine. ## Avec le coefficient directeur et de l’ordonnée à l’origine Une autre façon de représenter une fonction affine est de prendre en compte le coefficient directeur et l’ordonnée à l’origine. Connaître ces deux valeurs permet de déterminer l’allure générale de la droite. #
Comment déterminer une fonction affine ?
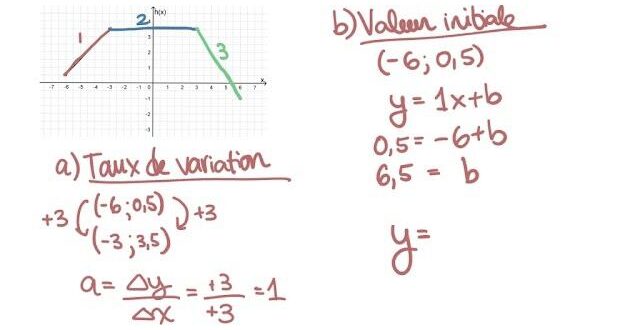
Il existe également plusieurs manières de déterminer une fonction affine. ## À partir de deux points sur un graphique Si l’on dispose de deux points distincts sur le graphique de la fonction, il est possible de déterminer la fonction affine qui les relie. En utilisant ces deux coordonnées, on peut calculer le coefficient directeur et l’ordonnée à l’origine, et ainsi établir une équation de la droite correspondante. ## Déterminer l’expression d’une fonction affine à partir d’un calcul Il est également possible de déterminer l’expression d’une fonction affine à partir de calculs mathématiques. Pour cela, il est nécessaire d’utiliser la formule générale f(x) = ax + b en identifiant les valeurs de a et b à partir des données fournies. #
Cas particulier de la fonction affine : la fonction linéaire
La fonction linéaire est un cas particulier de la fonction affine, pour laquelle l’ordonnée à l’origine est nulle. ## Définition de la fonction linéaire La fonction linéaire peut s’écrire sous la forme f(x) = ax, où a est le coefficient directeur. Dans ce cas, la fonction linéaire ne comporte pas de terme constant. ## Déterminer le coefficient d’une fonction linéaire Pour déterminer le coefficient d’une fonction linéaire, il suffit de regarder le nombre qui multiplie la variable x dans l’expression de la fonction. Cela correspond au coefficient directeur de la droite représentative. ## Représenter une fonction linéaire🔍 La représentation graphique d’une fonction linéaire est une droite passant par l’origine. Cette droite est caractérisée par sa pente, représentant le coefficient directeur a. #
Synthèse sur les fonctions affines 💭
– Une fonction affine est une fonction linéaire avec une translation. – On peut représenter une fonction affine à l’aide de deux points distincts ou en utilisant le coefficient directeur et l’ordonnée à l’origine. – Pour déterminer une fonction affine, on peut s’appuyer sur deux points sur un graphique ou effectuer des calculs pour identifier le coefficient a et l’ordonnée à l’origine b. – La fonction linéaire est un cas particulier de la fonction affine, caractérisée par l’absence d’ordonnée à l’origine. Leçons apprises : Comprendre le fonctionnement des fonctions affines est essentiel pour résoudre des problèmes mathématiques complexes et pour interpréter graphiquement des phénomènes du monde réel.
FAQ
Comment déterminer fonction ?
Une fonction est déterminée par une règle qui associe un élément d’un ensemble à un unique élément d’un autre ensemble. Elle peut être exprimée par une formule mathématique, un graphique ou un tableau. Pour la déterminer, il faut donc identifier cette règle d’association.
Comment trouver une fonction à partir de 2 points ?
Pour trouver une fonction linéaire à partir de deux points, utilisez la formule de la pente, (y2-y1)/(x2-x1), pour trouver la pente de la ligne. Ensuite, utilisez la formule y = mx + b (où m est la pente trouvé précédemment et b est l’ordonnée à l’origine) pour trouver l’équation de la ligne.