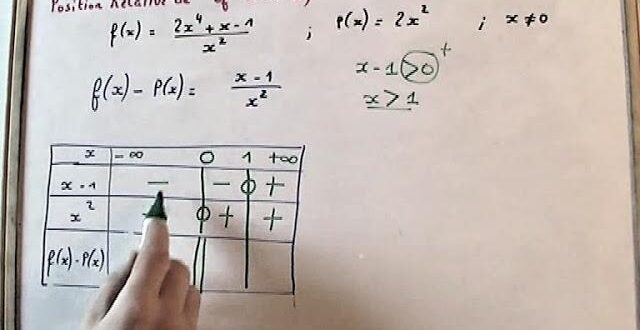Nos conseillers pédagogiques sont à votre écoute 7j/7
Savez-vous comment déterminer la position relative d’une courbe et de sa tangente ? Dans ce cours méthode, je vous explique tout, étape par étape.
La détermination de la position relative d’une courbe par rapport à sa tangente est un concept essentiel en mathématiques. Comprendre ce concept est crucial pour une meilleure compréhension de l’analyse de fonctions. Dans cet article, nous allons aborder les étapes clés pour étudier la position relative d’une courbe par rapport à sa tangente. Vous découvrirez comment rappeler l’équation de la tangente, calculer f(x) – (ax + b), étudier le signe de f(x) – (ax + b), et enfin conclure sur la position relative. Suivez-nous dans cette exploration pas à pas de ce sujet fondamental en mathématiques.
Rappeler l’équation de la tangente
Avant d’entrer dans les détails de la position relative d’une courbe par rapport à sa tangente, rappelons d’abord l’équation de la tangente. L’équation de la tangente à une courbe en un point donné se définit par la ligne droite qui touche la courbe en ce point. En d’autres termes, l’équation de la tangente représente la meilleure approximation linéaire de la courbe au voisinage du point d’intersection. Cette équation est mathématiquement définie par la forme y = ax + b, où a est la pente de la tangente et b est l’ordonnée à l’origine. Comprendre cette équation est crucial pour la suite de notre étude sur la position relative d’une courbe par rapport à sa tangente.
Calculer f(x) – (ax + b)
Une fois que l’équation de la tangente est rappelée, nous pouvons passer à l’étape suivante : le calcul de f(x) – (ax + b). Cette étape consiste à évaluer l’écart entre la fonction f(x) et la tangente représentée par l’équation ax + b. En d’autres termes, il s’agit de mesurer la différence entre la courbe réelle et son approximation linéaire représentée par la tangente. Ce calcul nous fournit des informations cruciales sur la position relative de la courbe par rapport à sa tangente. Comprendre ce calcul est nécessaire pour une analyse approfondie de la position relative.
Étudier le signe de f(x) – (ax + b)
Une fois que f(x) – (ax + b) est calculé, vient l’étape d’étudier le signe de cette différence. Étudier le signe de f(x) – (ax + b) nous permet de déterminer dans quelle mesure la courbe se trouve au-dessus ou en dessous de sa tangente à chaque point d’intérêt. Cette analyse de signe est essentielle pour déterminer la position relative de la courbe par rapport à sa tangente. Comprendre cette étape est crucial pour une analyse complète et précise de la position relative d’une courbe.
Conclure sur la position relative
Après avoir effectué les étapes précédentes, nous sommes prêts à conclure sur la position relative d’une courbe par rapport à sa tangente. En utilisant les informations obtenues à partir de l’équation de la tangente, du calcul de f(x) – (ax + b) et de l’analyse de signe, nous pouvons tirer des conclusions précises sur la position relative de la courbe. Cette conclusion nous permet de déterminer si la courbe se situe au-dessus, en dessous ou tangentiellement par rapport à sa tangente. Comprendre cette conclusion est fondamental pour une compréhension approfondie de la position relative d’une courbe par rapport à sa tangente.
| Étapes | Détails |
|---|---|
| Rappeler l’équation de la tangente | Équation de la tangente : y = ax + b |
| Calculer f(x) – (ax + b) | Mesure de l’écart entre la fonction et sa tangente |
| Étudier le signe de f(x) – (ax + b) | Analyse du positionnement relatif de la courbe |
| Conclure sur la position relative | Détermination finale de la position de la courbe |
Leçons apprises En conclusion, étudier la position relative d’une courbe par rapport à sa tangente est une étape fondamentale en mathématiques. En rappelant l’équation de la tangente, calculant f(x) – (ax + b), étudiant le signe de cette différence, et enfin en concluant sur la position relative, nous obtenons une compréhension approfondie de ce concept. La maîtrise de ces étapes est essentielle pour une analyse précise des fonctions et de leurs comportements locaux. La position relative d’une courbe par rapport à sa tangente est un domaine fascinant des mathématiques qui mérite d’être étudié en détail.
FAQ
Comment déterminer la position relative des courbes ?
La position relative des courbes est déterminée en étudiant les points d’intersection. Si deux courbes se coupent, elles sont dites sécantes. Si elles ne se coupent pas, elles sont soit parallèles, soit disjointes. On utilise également des équations pour analyser leur position.
Comment trouver position relative ?
La position relative se détermine en comparant la position d’un objet par rapport à un autre. Ceci peut être accompli en utilisant des points de référence, des directions (nord, sud, ouest, est) ou des mesures (mètres, kilomètres). Par exemple, une maison peut être à l’est d’une école, ou 2 km au sud d’un supermarché.
Comment étudier la position relative d’une droite ?
Pour étudier la position relative d’une droite, il faut d’abord identifier son équation, puis déterminer si une autre droite ou un point est sur cette droite, en parallèle, ou en intersection, en utilisant leurs équations respectives. Cette étude est généralement réalisée en utilisant les règles et les formules de la géométrie analytique.
Comment étudier la position d’une courbe par rapport à une tangente ?
On étudie la position d’une courbe par rapport à une tangente en utilisant le calcul différentiel. On détermine d’abord l’équation de la tangente en un point donné de la courbe en utilisant la dérivée de la fonction qui décrit la courbe. Ensuite, on compare les valeurs de la fonction et de sa tangente pour des points proches afin de déterminer la position relative de la courbe par rapport à la tangente.