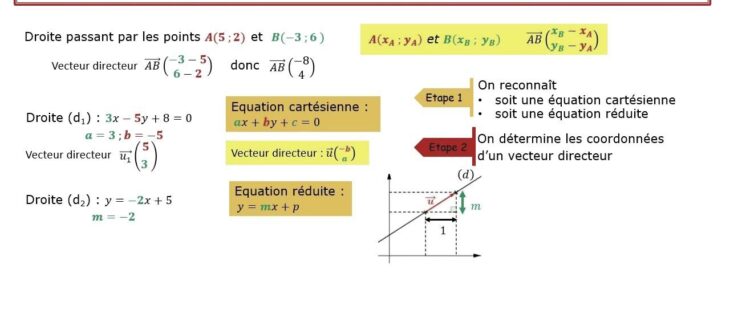
La recherche d’un vecteur directeur est une étape clé en mathématiques, en particulier en géométrie et en algèbre linéaire. Un vecteur directeur est un vecteur qui donne la direction d’une droite, d’un plan ou d’une courbe dans l’espace. Trouver un vecteur directeur peut sembler compliqué, mais avec les bonnes méthodes et connaissances, cela peut être abordé de manière systématique.
Compréhension des Vecteurs
Avant de plonger dans la recherche d’un vecteur directeur, il est crucial de comprendre en profondeur ce qu’est un vecteur et comment il est représenté. Un vecteur est une entité mathématique qui a à la fois une magnitude (ou norme) et une direction. En deux dimensions, un vecteur est communément représenté par une flèche du point de départ au point d’arrivée. En trois dimensions, un vecteur est souvent représenté par des coordonnées (x, y, z) dans un espace tridimensionnel.
Pour comprendre la recherche d’un vecteur directeur, il est nécessaire de maîtriser les opérations sur les vecteurs, notamment l’addition, la soustraction, la multiplication par un scalaire et le produit scalaire. Ces opérations sont essentielles pour manipuler les vecteurs et les utiliser dans divers contextes mathématiques et scientifiques.
Méthodes pour Trouver un Vecteur Directeur
Il existe plusieurs méthodes pour trouver un vecteur directeur , en fonction du contexte et de la situation spécifique. L’une des méthodes les plus courantes consiste à utiliser les coordonnées des points à travers lesquels passe la droite, le plan ou la courbe en question. Cette approche implique de calculer la différence entre les coordonnées pour obtenir un vecteur qui indique la direction souhaitée.
Une autre méthode courante consiste à utiliser des concepts plus avancés tels que les dérivées partielles pour les courbes dans l’espace ou les calculs de produit vectoriel pour les plans. Ces méthodes requièrent une compréhension approfondie du calcul vectoriel et de l’algèbre linéaire, mais elles peuvent fournir des résultats précis et significatifs dans des contextes plus complexes.
Exemples Pratiques
Pour illustrer ces méthodes, considérons un exemple concret. Supposons que nous avons une droite dans l’espace définie par les points A(1, 2, 3) et B(4, 5, 6). Pour trouver un vecteur directeur de cette droite, nous pouvons soustraire les coordonnées de ces deux points pour obtenir un vecteur qui pointe dans la direction de la droite.
Dans un autre cas, si nous travaillons avec un plan défini par une équation comme ax + by + cz = d, nous pouvons utiliser les coefficients a, b et c de l’équation pour obtenir un vecteur normal au plan, qui peut également servir de vecteur directeur.
Considérations Supplémentaires
Lors de la recherche d’un vecteur directeur , il est important de prendre en compte les cas particuliers et les exceptions qui peuvent survenir. Certains objets mathématiques, tels que les courbes paramétriques, peuvent nécessiter des approches spécifiques pour trouver un vecteur directeur valide. De plus, la compréhension de la nature géométrique des objets en question est essentielle pour interpréter correctement les vecteurs directeurs obtenus.
En résumé, la recherche d’un vecteur directeur est une compétence fondamentale dans divers domaines mathématiques et scientifiques, et elle repose sur une compréhension solide des vecteurs, des opérations vectorielles et des méthodes spécifiques adaptées au contexte. Avec la pratique et la maîtrise de ces concepts, la recherche de vecteurs directeurs deviendra plus intuitive et efficace.
Réflexions Finales
En conclusion, la recherche d’un vecteur directeur implique la compréhension des concepts fondamentaux des vecteurs, des opérations vectorielles et des méthodes spécifiques adaptées à chaque situation. En suivant des étapes systématiques et en utilisant les bonnes méthodes, il est possible de trouver des vecteurs directeurs précis et significatifs pour représenter la direction d’objets mathématiques dans l’espace. Cette compétence est essentielle pour de nombreuses applications mathématiques, scientifiques et techniques, et elle ouvre la voie à une compréhension plus approfondie de la géométrie et de l’algèbre linéaire.
| Méthodes | Exemples | Considérations |
|---|---|---|
| Coordonnées des points | Droites, Plans | Cas particuliers |
| Calculs avancés | Courbes paramétriques | Exceptions |
FAQ
Comment trouver un vecteur directeur à partir d’une équation ?
Pour trouver un vecteur directeur à partir d’une équation linéaire de la forme y = mx + p, le vecteur directeur est simplement (1, m). Si l’équation est dans le format général ax + by + c = 0, alors le vecteur directeur est (a, b). Cela décrit la direction de la ligne sur le plan cartésien.
Quel est le vecteur directeur d’une droite ?
Un vecteur directeur d’une droite est un vecteur qui donne la direction de cette droite. C’est donc un vecteur parallèle à la droite. Il existe une infinité de vecteurs directeurs pour une même droite, obtenus en multipliant ou divisant un vecteur directeur par un réel non nul.
Quel est le vecteur directeur d’un plan ?
Un plan n’a pas un seul vecteur directeur, mais une infinité. Ces vecteurs directeurs sont tous les vecteurs non nuls et parallèles au plan. Ils donnent la direction générale du plan.