ENTETE
Le calcul du produit scalaire est un outil puissant en mathématiques, souvent utilisé en géométrie et en physique. Il permet de mesurer la similarité entre deux vecteurs et de déterminer l’angle entre eux. Dans cet article, nous allons explorer différentes méthodes pour calculer le produit scalaire, en utilisant des approches telles que la projection orthogonale, les formules trigonométriques, les normes de vecteurs, les repères orthonormés et la relation de Chasles.
Propriété
Avant d’explorer les différentes méthodes de calcul du produit scalaire, il est important de rappeler la définition de cette opération mathématique. Le produit scalaire de deux vecteurs est une opération algébrique qui prend deux vecteurs comme entrée et renvoie un scalaire comme résultat. Il est souvent noté de la forme a.b ou .
1. Utiliser une projection orthogonale
Théorème
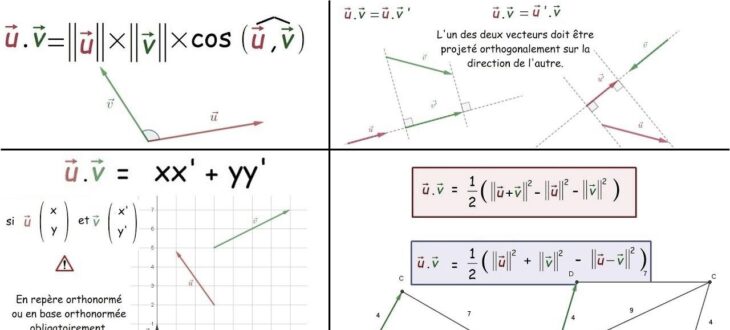
La projection orthogonale est une méthode puissante pour calculer le produit scalaire. Cette approche utilise la notion de projection d’un vecteur sur un autre. Le produit scalaire peut être obtenu en multipliant la norme du vecteur projeté par la norme du vecteur sur lequel la projection est effectuée, puis en multipliant le résultat par le cosinus de l’angle entre les deux vecteurs.
Remarque
Il est important de noter que la projection orthogonale permet de calculer le produit scalaire de manière intuitive, en visualisant la composante commune des deux vecteurs. Cette méthode est largement utilisée dans les applications pratiques, telles que la mécanique des solides, la géométrie analytique et la physique.
Exemple
Prenons par exemple deux vecteurs a et b dans un espace tridimensionnel. La projection orthogonale nous permet de calculer leur produit scalaire en utilisant la formule :
| Vecteur | Norme |
|---|---|
| a | ||a|| |
| b | ||b|| |
2. Appliquer une formule utilisant le cosinus d’un angle
Définition
Une autre approche pour calculer le produit scalaire consiste à utiliser une formule basée sur le cosinus de l’angle entre les deux vecteurs. Cette méthode fait appel à la relation trigonométrique entre le produit scalaire, les normes des vecteurs et l’angle entre eux.
Remarque
Il est intéressant de noter que cette méthode offre une alternative intuitive pour calculer le produit scalaire sans recourir à la projection orthogonale. Elle est particulièrement utile lorsqu’il est difficile de visualiser la projection des vecteurs dans l’espace.
Exemple
Considérons deux vecteurs u et v dans un espace vectoriel. En utilisant la formule du produit scalaire basée sur le cosinus de l’angle entre les deux vecteurs, nous pouvons obtenir le résultat en utilisant l’expression suivante :
3. Appliquer une formule utilisant les normes de 3 vecteurs
Théorème
Une autre méthode pour calculer le produit scalaire fait appel aux normes des vecteurs impliqués. En utilisant la relation entre les normes des vecteurs et l’angle entre eux, il est possible de dériver une formule pour calculer le produit scalaire de manière efficace.
Exemple
Supposons trois vecteurs x , y et z dans un espace vectoriel. En appliquant la formule basée sur les normes des vecteurs, nous pouvons calculer le produit scalaire en utilisant la relation suivante :
4. Se placer dans un repère orthonormé
Théorème
Le repère orthonormé fournit un cadre mathématique particulièrement adapté pour le calcul du produit scalaire. En se plaçant dans un tel repère, les coordonnées des vecteurs peuvent être utilisées pour déterminer le produit scalaire de manière aisée et efficace.
Remarque
L’utilisation d’un repère orthonormé simplifie grandement le calcul du produit scalaire, car elle permet de représenter les vecteurs sous forme de coordonnées numériques dans un espace cartésien.
Exemple
En se plaçant dans un repère orthonormé, le calcul du produit scalaire de deux vecteurs a et b peut se faire en utilisant la formule suivante :
5. Utiliser la relation de Chasles
Propriété
La relation de Chasles offre une méthode alternative pour calculer le produit scalaire. Cette approche repose sur la décomposition d’un vecteur en la somme de deux autres vecteurs et l’utilisation de la linéarité du produit scalaire.
Remarque
L’utilisation de la relation de Chasles peut s’avérer utile dans des contextes où les vecteurs peuvent être décomposés en termes plus simples, facilitant ainsi le calcul du produit scalaire.
Exemple
En utilisant la relation de Chasles, le produit scalaire de deux vecteurs p et q peut être calculé en utilisant la formule suivante :
Dans ce chapitre :
Cours
– Définition du produit scalaire – Propriétés du produit scalaire – Utilisation de la projection orthogonale – Formulaire basée sur le cosinus d’un angle – Formulaire basée sur les normes de 3 vecteurs – Utilisation d’un repère orthonormé – Relation de Chasles
Exercices
– Exercice 1 : Calcul du produit scalaire de deux vecteurs donnés – Exercice 2 : Application de la projection orthogonale pour calculer le produit scalaire – Exercice 3 : Utilisation des formules trigonométriques pour le produit scalaire
Méthodes
– Méthode 1 : Projection orthogonale en pratique – Méthode 2 : Utilisation des formules trigonométriques – Méthode 3 : Application des normes de vecteurs pour le calcul du produit scalaire
Quiz
Testez vos connaissances sur le calcul du produit scalaire avec notre quiz interactif ! [‘Prochaines étapes’] Après avoir exploré les différentes méthodes de calcul du produit scalaire, il est important de pratiquer ces concepts à travers des exercices et des problèmes concrets. La manipulation des formules et des méthodes présentées dans cet article permettra de consolider vos connaissances et de les appliquer à des problèmes réels en mathématiques et en physique.
FAQ
Comment on calcule le produit scalaire de deux vecteurs ?
On calcule le produit scalaire de deux vecteurs en multipliant chaque composante correspondante des deux vecteurs et en additionnant ces produits. En notation mathématique : si A = (a1, a2, a3) et B = (b1, b2, b3) sont deux vecteurs, leur produit scalaire est a1*b1 + a2*b2 + a3*b3.
Comment calculer la norme produit scalaire ?
La norme d’un vecteur dans un espace doté d’un produit scalaire est calculée en prenant la racine carrée du produit scalaire de ce vecteur avec lui-même. Mathématiquement, pour un vecteur ‘v’, sa norme (||v||) est donnée par √(v.v) où ‘.’ désigne le produit scalaire.
Comment calculer un produit scalaire avec des longueurs ?
On calcule un produit scalaire avec des longueurs en multipliant la longueur de chaque dimension correspondante entre les deux vecteurs. Ensuite, on additionne tous ces produits pour obtenir le produit scalaire. C’est-à-dire si les vecteurs sont A = (a1, a2,…,an) et B = (b1, b2,…,bn), alors le produit scalaire est a1*b1 + a2*b2 +…+ an*bn.
Comment calculer le produit scalaire dans un rectangle ?
La notion de produit scalaire n’est pas spécifique à un rectangle. C’est une opération entre deux vecteurs. Dans un espace à 2 dimensions, le produit scalaire de deux vecteurs A et B est calculé en multipliant les composantes correspondantes de A et B et en additionnant les résultats (AxB = Ax*Bx + Ay*By). Dans le cas d’un rectangle, vous pouvez utiliser le produit scalaire pour calculer l’angle entre deux côtés ou l’orthogonalité de deux côtés, en sachant que le produit scalaire de deux vecteurs orthogonaux est nul.