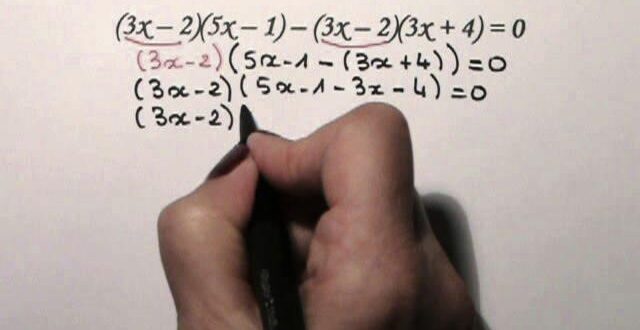Nos conseillers pédagogiques sont à votre écoute 7j/7
Lorsqu’on est confronté à une équation produit nul, il est crucial de savoir comment la résoudre. Que ce soit dans le cadre scolaire ou professionnel, la maîtrise de cette méthode est essentielle. Dans cet article, nous allons explorer en détail les étapes à suivre pour résoudre une équation produit nul. À la fin de la lecture, vous aurez acquis les connaissances nécessaires pour aborder ce type de problème avec assurance.
Comprendre le concept d’équation produit nul
Avant d’aborder la résolution des équations produit nul, il est important de comprendre ce que représente ce type d’équation. Une équation produit nul est une équation qui peut être factorisée en une multiplication égale à zéro. En d’autres termes, pour résoudre une équation produit nul, il faut trouver les valeurs des variables qui rendent le produit égal à zéro.
Supposons que nous ayons l’équation (x-3)(x+2) = 0. Pour la résoudre, nous devons trouver les valeurs de x qui annulent le produit (x-3)(x+2). Cela nous amène à la première étape de la résolution : la factorisation.
Étapes de résolution
La résolution d’une équation produit nul passe par plusieurs étapes clés. La première consiste à factoriser l’équation donnée. Dans notre exemple, nous factorisons (x-3)(x+2) pour obtenir les facteurs individuels. Une fois la factorisation effectuée, nous égalons chaque facteur à zéro et résolvons les équations obtenues. Ces solutions correspondent aux valeurs de la variable qui annulent le produit, et sont donc les solutions de l’équation produit nul.
Par exemple, pour notre équation (x-3)(x+2) = 0, nous factorisons pour obtenir x-3 = 0 et x+2 = 0. En résolvant ces équations, nous trouvons que x = 3 et x = -2. Ces deux valeurs sont les solutions de notre équation produit nul.
Exemples pratiques de résolution
Pour bien comprendre la méthode de résolution des équations produit nul, voyons quelques exemples concrets. Considérons l’équation 2x(x-4) = 0. La première étape consiste à factoriser le membre de gauche pour obtenir 2x = 0 et x-4 = 0. En résolvant ces équations, nous trouvons que x = 0 et x = 4. Ce sont les solutions de notre équation produit nul.
Un autre exemple intéressant est l’équation (y+5)(y-7) = 0. Encore une fois, nous factorisons pour obtenir y+5 = 0 et y-7 = 0. Les solutions de ces équations sont y = -5 et y = 7, qui sont les solutions de l’équation produit nul.
Techniques avancées
En dehors des cas simples, il existe des techniques avancées pour résoudre des équations produit nul plus complexes. Ces techniques incluent l’utilisation de formules quadratiques et la méthode de substitution. Dans chaque cas, l’objectif est de simplifier l’équation et d’isoler les solutions.
Par exemple, pour l’équation 3x^2 – 12x = 0, nous pouvons utiliser la formule quadratique pour trouver les solutions. De même, pour l’équation (2a-1)(a+5) = a^2+9, la méthode de substitution peut être utilisée pour résoudre l’équation produit nul.
Réflexions finales
En conclusion, la résolution d’une équation produit nul est une compétence fondamentale en mathématiques. En comprenant le concept et en suivant les étapes de résolution, vous serez en mesure de résoudre efficacement ce type d’équation. En pratiquant sur différents exemples, vous renforcerez votre compréhension et gagnerez en confiance dans vos capacités. Si vous rencontrez des difficultés, n’hésitez pas à demander de l’aide à nos conseillers pédagogiques, disponibles 7j/7 pour répondre à vos questions.
| Titre | Contenu |
|---|---|
| Comprendre le concept d’équation produit nul | Explication du concept d’équation produit nul et son application. |
| Étapes de résolution | Détail des étapes à suivre pour résoudre une équation produit nul. |
| Exemples pratiques de résolution | Illustration de la méthode à travers des exemples concrets. |
| Techniques avancées | Exploration des techniques avancées pour résoudre des équations produit nul plus complexes. |
| Réflexions finales | Conseils et encouragement pour renforcer les compétences de résolution. |